7.26.4.2 AL/Algoritmos Fundamentales. (16 horas) [Nivel Bloom 5]

Referencias Bibliográficas: [,,]

Tópicos

1. Algoritmos numéricos simples.
2. Búsqueda secuencial y binaria.
3. Algoritmos cuadráticos de ordenamiento (selección, inserción).
4. Algoritmos de tipo 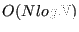$O(N log N)$ (Quicksort, heapsort, mergesort).
5. Tablas de (hash) incluyendo estrategias de solución para las colisiones.
6. Árboles de búsqueda binaria.
7. Representación de grafos (Listas y Matrices de adyacencia).
8. Recorridos por amplitud y profundidad.
9. El algoritmo del camino más corto (algoritmos de Dijkstra y Floyd).
10. Cerradura transitiva (algoritmo de Floyd).
11. Árbol de expansión mínima (algoritmos de Kruskal y Prim).
12. Ordenamiento Topológico.

Objetivos

1. Implementar los algoritmos cuadráticos más comunes y los algoritmos de ordenamiento $O(N log N)$.
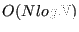2. Diseñar e implementar una función de (hash) apropiada para una aplicación.
3. Diseñar e implementar un algoritmo de resolución de colisiones para tablas de hash.
4. Discutir la eficiencia computacional de los principales algoritmos de ordenamiento, búsqueda y (hashing).
5. Discutir otros factores, además de la eficiencia computacional, que influyen en la elección de los algoritmos, tales como tiempo de programación, mantenimiento y el uso de patrones específicos de aplicación en los datos de entrada.
6. Resolver problemas usando los algoritmos de grafos fundamentales, incluyendo búsqueda por amplitud y profundidad; caminos más cortos con uno y múltiples orígenes, cerradura transitiva, ordenamiento topológico y al menos un algoritmo de árbol de expansión mínima.
7. Demostrar las siguientes capacidades: evaluar algoritmos, seleccionar una opción de un rango posible, proveer una justificación para tal elección e implementar el algoritmo..